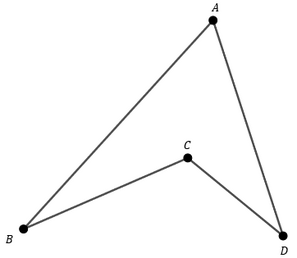
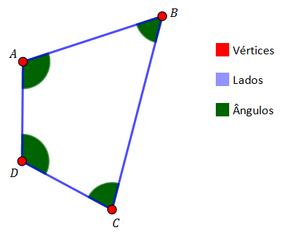
Quadriláteros

Quadrilátero é um polígono de quatro lados. Em outras palavras, um quadrilátero é uma figura formada por quatro pontos $A, B, C$ e $D$ (de forma que não existe três destes que são alinhados) e pelos segmentos $AB,BC,CD$ e $DA$, de modo que os segmentos $AB$ e $CD$ não possuem nenhum ponto em comum (e o mesmo ocorre com $BC$ e $DA$).

Nesta definição, $A, B, C$ e $D$ são chamados de vértices e $AB,BC,CD$ e $DA$ são chamados de lados. Podemos denotar um quadrilátero de vértices $A$, $B$, $C$ e $D$ por $\square ABCD$ ou $\# ABCD$.

Em um quadrilátero, dois lados são chamados de opostos se não possuem nenhum vértice em comum. Por exemplo, na figura anterior, os lados $AB$ e $CD$ são opostos. O mesmo ocorre os lados $BC$ e $DA$.

Os segmentos que unem vértices mas não são lados são chamados de diagonais.

Um quadrilátero é chamado convexo se não possuir nenhum ângulo maior do que $180^{\circ}$. Caso contrário, ele é chamado de côncavo.

Proposição

A soma das medidas dos ângulos internos de um quadrilátero convexo é igual a $360^{\circ}$.

Trapézios

São quadriláteros que possuem pelo menos um par de lados opostos paralelos. Os lados paralelos são chamados de base. Os outros dois lados são chamados de laterais.

Em um trapézio, um segmento que sai de uma base e chega na outra formando $90^\circ$ é chamado de altura.

Se um trapézio possuir suas laterais de mesma medida, iremos dizer que ele é isósceles.

Um trapézio é retângulo quando as duas bases possuem ângulos retos adjacentes a eles e estes são consecutivos.

Proposição

Seja $ABCD$ um quadrilátero que não é um paralelogramo. Então $ABCD$ é um trapézio isósceles de bases $AB$ e $CD$ se, e somente se, $\angle A = \angle B$ e $\angle C = \angle D$.

Observação

A recíproca da afirmação anterior é válida mesmo quando $ABCD$ é um paralelogramo.

Propriedades

• Se um trapézio isósceles não é um paralelogramo, então as suas diagonais possuem o mesmo tamanho.

• Sejam $ABCD$ um quadrilátero e $E$ o encontro das suas diagonais. Se $EA=EB$ e $EC=ED$, então $ABCD$ é um trapézio isósceles.

Exemplo

Seja $ABCD$ um trapézio isósceles (com $AB$ paralelo a $CD$) e $E$ o ponto de encontro entre as diagonais $AC$ e $BD$. Prove que $EA=EB$ e $EC=ED$.

Solução: Seria legal se conseguíssemos uma congruência envolvendo $EA$, $EB$, $EC$ e $ED$. Possíveis candidatos são os triângulos $AED$ e $BEC$. Observe que $AD=BC$ e não conseguimos falar muito mais sobre lados. Vamos atacar com ângulos. Observe que $\angle AED=\angle BEC$. Se mostrarmos que $\angle DAE=\angle CBE$, os triângulos serão congruentes e as igualdades do enunciado serão verdadeiras.

Para mostrarmos que essa última igualdade é verdadeira, vamos encontrar uma congruência que envolve esses ângulos. Observe os triângulos $DAC$ e $CBD$. Repare que $DA=CB$ e $CD$ é um lado comum. Além disso, $\angle ADC=\angle BCD$. Logo os triângulos são congruentes pelo caso $LAL$ e assim:

$\angle DAE=\angle DAC=\angle CBD=\angle CBE.$

Assim $AED$ e $BEC$ são congruentes e com isso $EA=EB$ e $EC=ED$.

Paralelogramos

São quadriláteros que possuem lados opostos paralelos.

Todo paralelogramo é um trapézio. Apesar de que existem autores que consideram que paralelogramos não são trapézios.

Vantagens de Termos um Paralelogramo na Figura

• Ganhamos paralelismos
• Ganhamos medidas iguais
• Se soubermos uma das medidas, podemos saber todas as outras.

Proposição

(i) Um quadrilátero é um paralelogramo se, e somente se, os dois pares de lados opostos possuem mesmo comprimento.

(ii) Um quadrilátero é um paralelogramo se, e somente se, seus dois pares de ângulos opostos possuem mesma medida.

(iii) As diagonais de um quadrilátero se cruzam no ponto médio se, e somente se, ele for um paralelogramo.

(iv) Os ângulos consecutivos de um quadrilátero são suplementares se, e somente se, ele é um paralelogramo.

(v) Se um quadrilátero possuir um par de lados opostos paralelos e de mesma medida, então este quadrilátero é um paralelogramo.

(vi) As diagonais de um quadrilátero o divide em quatro triângulos de mesma área se, e somente se, ele for um paralelogramo.

Exemplo

Sejam $ABCD$ um quadrilátero e $M$ o ponto de encontro das diagonais. Se $AB$ e $CD$ são paralelos, $M$ é o ponto médio de $AC$, prove que $ABCD$ é um paralelogramo.

Solução: Como $\angle BAM=\angle DCM$ (pois $AB$ e $CD$ são paralelos), $AM=MC$ (pois $M$ é ponto médio de $CD$) e $\angle AMB=\angle CMD$, segue que os triângulos $ABM$ e $CDM$ são congruentes pelo caso $ALA$. Desta forma, $BM=DM$. Como as suas diagonais se encontram nos seus pontos médios, segue que $ABCD$ é um paralelogramo.

Losangos

Losango é um quadrilátero em que todos os lados possuem mesma medida.

Todo losango é também um paralelogramo.

Proposição

(i) As diagonais de um losango são perpendiculares entre si.

(ii) As diagonais de um losango dividem-o em quatro triângulos congruentes.

(iii) As diagonais de um quadrilátero dividem seus quatros ângulos ao meio se, e somente se, ele é um losango.

(iv) Se as diagonais de um paralelogramo são perpendiculares e se dividem ao meio, então ele é um losango.

Retângulos

Um quadrilátero é um retângulo se todos os seus ângulos medirem $90^\circ$.

Em um retângulo, os lados ganham os nomes de largura e comprimento. A largura é sempre menor do que o comprimento.

Observação

Todo retângulo é um paralelogramo. Então toda propriedade de um paralelogramo também é propriedade de um retângulo.

Proposição

(i) As diagonais de um retângulo têm mesma medida.

(ii) Se as diagonais de um quadrilátero são congruentes e se cortam nos seus pontos médios, então ele é um retângulo.

(iii) Se as diagonais de um paralelogramo são congruentes, então ele é um retângulo.

Quadrado

Um quadrado é um quadrilátero que possui todos os lados de mesmo tamanho e todos os ângulos medindo $90^\circ$.

Todo quadrado é um losango e um retângulo ao mesmo tempo.

Proposição

Se as diagonais de um quadrilátero possuem mesmo tamanho, se encontram no ponto médio e são perpendiculares entre si, então ele é um quadrado.

Resumo da Classificação dos Quadriláteros

Caso você queira organizar melhor seu raciocínio, a seguir temos uma representação:

Exemplo

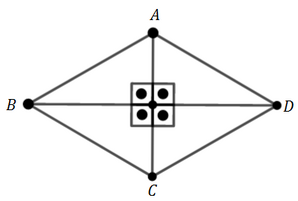
Um quadrilátero menos conhecido é o deltoide (ou também chamado de pipa). Você não precisa guardá-lo, mas vale a pena mexermos um pouco com ele.

A definição de deltoide é a seguinte: é um quadrilátero de dois pares disjuntos de lados adjacentes congruentes. Como assim? Observe os dois pares de lado $AB$ e $AD$ e outro par $CB$ e $CD$. Eles são disjuntos, pois não existe nenhum lado que está nos dois pares ao mesmo tempo. São adjacentes, pois possui um vértice em comum (de fato, $AB$ e $AD$ possuem o vértice $A$ em comum, enquanto $CB$ e $CD$ possuem o vértice $C$ em comum). E eles são congruentes pois $AB=AD$ e $CB=CD$. Vamos provar algumas propriedades sobre ele. Considere $E$ o ponto de encontro entre as diagonais.

(a) Prove que a diagonal $AC$ é bissetriz dos ângulos $\angle BAD$ e $\angle BCD$.

(b) Prove que as diagonais são perpendiculares.

(c) Prove que $BE=ED$.

(d) Prove que $\angle ABC=\angle ADC$.

(e) Se $AC=d_1$ e $BD=d_2$, prove que a área de $ABCD$ é $\frac{d_1d_2}{2}$.

Solução:

(a) Observe que os triângulos $ABC$ e $ADC$ são congruentes pelo caso $LLL$ (já que $AB=AD$, $BC=DC$ e $AC$ é um lado comum). Desta forma, $\angle BAC=\angle DAC$, ou seja, $AC$ é bissetriz de $\angle BAD$. Além disso, pela mesma congruência, $\angle BCA=\angle DCA$, ou seja, $AC$ é bissetriz de $\angle BCD$.

Note que não podemos falar que $BD$ é bissetriz $\angle ABC$ e $\angle ADC$. Aliás só poderíamos falar isso quando $ABCD$ fosse um losango.

(b) Observe que o triângulo $ABD$ é isósceles de base $BD$. Como $AE$ é bissetriz, segue que ela também é altura e assim as diagonais são perpendiculares.

(c) Ainda no triângulo $ABD$, como $AE$ é bissetriz e altura, segue que também é mediana e assim $BE=ED$.

(d) Como provamos no item (a), os triângulos $ABC$ e $ADC$ são congruentes e assim $\angle ABC=\angle ADC$.

(e) Considere $x=AE$ e $y=CE$. Observe que $x+y=d_1$. Assim

$[ABCD]=[ABD]+[BCD]=\frac{d_2x}{2}+\frac{d_2y}{2}=\frac{(x+y)d_2}{2}=\frac{d_1d_2}{2}.$

Exemplo

Na figura, prove que $\angle BCD=\angle ABC+\angle CDA + \angle DAB$.

Observação: Nas soluções a seguir, tome $\alpha=\angle BAD$, $\beta=\angle ABE$ e $\gamma=\angle CDA$

Solução 1: É mais fácil mexermos com triângulos do que com quadriláteros. Por isso, vamos dividir a nossa figura em triângulos. Considere $E$ o ponto de encontro entre as retas $BC$ e $AD$. Pelo Teorema do Ângulo Externo no triângulo $ABE$, podemos concluir que $\angle CED=\alpha+\beta$. Além disso, se usarmos o Teorema do Ângulo Externo no triângulo $CED$ e assim $\angle BCD=\alpha+\beta+\gamma$.

Observação: Conseguimos uma solução análoga se tomarmos $E$ o ponto de encontro entre $AB$ e $CD$.

Solução 2: Seja $x=\angle BCD$. Também temos o ângulo $\angle BCD$ que está interno ao quadrilátero $ABCD$ e mede $360^{\circ}-x$. Como a soma dos ângulos de um quadrilátero é $360^{\circ}$, segue que

$\alpha+\beta+\gamma+360^{\circ}-x=360^{\circ} \Leftrightarrow x=\alpha+\beta+\gamma.$

Solução 3: Seja $F$ um ponto na reta $AC$ de forma que $C$ esteja entre $A$ e $F$. Considere $\theta=\angle BAF$. Então $\angle FAD=\alpha-\theta$. Se aplicarmos o Teorema do Ângulo Externo nos triângulos $ABC$ e $ACD$ iremos obter respectivamente $\angle BCF=\theta+\beta$ e $\angle FCD=\alpha-\theta+\gamma$. Daí $\angle BCD=\alpha+\beta+\gamma$.

Solução 4: Tome $\varphi=\angle CBD$ e $\omega=\angle CDB$. Como a soma dos ângulos internos do triângulo $ABD$ é $180^{\circ}$,

$\alpha+\beta+\gamma+\omega+\varphi=180^{\circ}$.

Se usarmos o mesmo resultado no triângulo $BCD$,

$\varphi+\omega+\angle BCD=180^{\circ}$.

Ao subtrairmos uma igualdade da outra

$\angle BCD=\alpha+\beta+\gamma.$

Exemplo

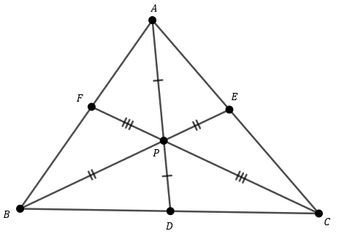
Prove que não existe um ponto $P$ no triângulo $ABC$, conforme a figura abaixo: $AP=PD$, $BP=PE$ e $CP=PF$.

Solução: Suponha, por absurdo, que ele exista. Observe que as diagonais de $AEDB$ se cortam em seus pontos médios e desta forma ele é um paralelogramo. Então $AE$ é paralelo a $BD$ e com isso $AC$ é paralelo a $BC$. Absurdo. Portanto, não existem pontos que satisfaçam as condições do enunciado.

Exemplo (Cone Sul 2006)

No quadrilátero convexo $ABCD$, sejam $E$ e $F$ os pontos médios dos lados $AD$ e $BC$, respectivamente. Os segmentos $CE$ e $DF$ cortam-se em $O$. Demonstrar que se as retas $AO$ e $BO$ dividem o lado $CD$ em três partes iguais então $ABCD$ é um paralelogramo.

Solução: Existem várias maneiras de provarmos que um quadrilátero é um paralelogramo. Mas ainda parece muito cedo: vamos encontrar mais informações sobre a figura.

Sejam $G$ e $H$, os pontos de intersecção de $CD$ com as retas $AO$ e $BO$, respectivamente.

Observe que $FG$ é base média do triângulo $CHB$ e com isso, os triângulos $DHO$ e $DGF$ são semelhantes. Assim

$\frac{DO}{DF}=\frac{DH}{DG} \Rightarrow DF = 2 DO \Rightarrow OF = DO.(*)$

Da mesma forma, $EH$ é base média do triângulo $DAG$, se onde segue que os triângulos $COG$ e $CEH$ são semelhantes. Desta forma,

$\frac{CO}{CE}=\frac{CG}{CH} \Rightarrow CE=2CO \Rightarrow OE=CO.(**)$

Por $(*)$ e $(**)$, as diagonais de $EFCD$ se encontram, de onde segue que ele é um paralelogramo. E o que ganhamos com isso? Aqui $ED$ e $FC$ serão paralelos, de onde segue que $AD$ e $BC$ são paralelos.

Se provarmos que $AD=BC$, conseguiremos ter mostrado que $ABCD$ é um paralelogramo. Mas esta igualdade segue dos fatos de que $ED=FC$ e $E$ e $F$ são pontos médios de $AD$ e $BC$, respectivamente.

Exemplo (Cone Sul 1989)

Seja $ABCD$ um quadrado com diagonais $AC$ e $BD$ e $P$ um ponto em um dos lados do quadrado. Mostre que a soma das distâncias de $P$ até as diagonais é constante.

Solução: Se mostrarmos que $P$ depende apenas da medida do lado do quadrado (que chamaremos de $l$), nosso problema estará resolvido. Suponha sem perda de generalidade que $P$ pertence ao segmento $AB$. Sejam $Q$ e $R$ pontos sobre $AC$ e $BD$, respectivamente, tais que $PQ$ e $PR$ são perpendiculares a $AC$ e $BD$, respectivamente. Mostraremos que $PQ+PR$ depende apenas de $l$.

Seja $O$ o ponto de encontro das diagonais. Os triângulos $AQP$ e $AOB$ são semelhantes, pois $QP$ e $OB$ são paralelos. Assim,

$\frac{PQ}{OB}=\frac{AP}{AB} \Leftrightarrow PQ= OB.\frac{AP}{AB}.$

Analogamente, como $BRP$ e $BOA$ são semelhantes, $PR=OA.\frac{BP}{AB}.$

Desta forma, como $OB=OA$,

$PQ+PR=OB.\frac{AP}{AB}+OA.\frac{BP}{AB}=\frac{OB}{AB}.(AP+BP)=OB=\frac{l\sqrt{2}}{2}.$

Portanto, $PQ+PR$ é constante.

Como usar as propriedades do quadrilátero a seu favor

Às vezes queremos provar que duas coisas são paralelas. Uma maneira interessante é encontrarmos paralelogramos na figura. Mas como provar que um quadrilátero é um paralelogramo? Uma maneira é ver que lados opostos possuem mesma medida.

Exemplo

Se $ABCDEF$ é um hexágono regular, mostre que $AF$ é paralelo a $CD$.

Solução: Mostraremos que $ACDF$ é um paralelogramo. Já sabemos que $AF=CD$. Se provarmos que $AC=DF$, $ACDF$ será um paralelogramo e com isso $AF$ será paralelo a $CD$.

Para mostrarmos esta igualdade, vamos usar congruências de triângulo. Observe que $AB=FE$ e $BC=ED$. Além disso, $\angle ABC= \angle FED$. Logo $ABC$ e $FED$ são congruentes pelo caso $LAL$. Logo, $AC=DF$.

Exemplo

Considere $ABCDEF$ um hexágono de forma que as diagonais $AD,BE$ e $CF$ se encontram em $M$ que é ponto médio destes três segmentos. Prove que $AB = DE$, $BC=EF$ e $ED=FA$.

Solução: Sabemos que se as diagonais de um quadrilátero se encontram no seu ponto médio, então ele é um paralelogramo. E isto é bom, pois as diagonais dos quadriláteros $ABDE,BCEF$ e $CDFA$ se encontram nos pontos médios, de onde segue que eles são paralelogramos. Daí $AB = DE$, $BC=EF$ e $ED=FA$.

Exemplo

Sejam $ABC$ um triângulo e $X$ um ponto sobre o lado $BC$. Se $AX$ é mediana e bissetriz, então o triângulo é isósceles.

Solução: Parece que não é possível encontrar uma congruência entre os triângulos $ABM$ e $ACM$. Por isso, vale a pena procurarmos outra estratégia. A questão é: como vamos usar que $X$ é ponto médio de $BC$? Quais resultados você conhece sobre pontos médios? Uma deles pode ser o seguinte: as diagonais de um paralelogramo se encontram nos seus pontos médios. Mas para podermos usar isso, deveríamos ter dois segmentos se cortando em um ponto médio. Se não está do jeito que queremos, podemos forçar: prolongue $AX$ por $X$ até o ponto $D$ de forma que $AX=XD$.

O que ganhamos com isso? Observe o quadrilátero $ABDC$. As suas diagonais ($AD$ e $BC$) se encontram em seus pontos médios. Logo, ele é um paralelogramo. E o que ganhamos com isso? Várias propriedades. Como ainda não usamos o fato de que $AX$ é bissetriz, considere $\alpha=\angle BAX=\angle XAC$. Como $AC$ é paralelo a $BD$, podemos concluir que $\angle ADB=\alpha$. Assim, se aplicarmos o Teorema do Triângulo Isósceles no triângulo $ABD$, iremos obter $AB=BD$. Mas $AC=BD$. Desta forma, $AB=AC$ e por isso o triângulo $ABC$ é isósceles de base $BC$.

Exemplo

Sejam $ABC$ um triângulo e $AM$ a sua mediana. Prolongue $AM$ por $M$ até o ponto $D$ de forma que $\angle DBA$ seja um ângulo reto. Se $\angle MAC = 2\angle BAM$, prove que $AC=\frac{1}{2}AD$.

Solução: Parece chato provar que $AC=\frac{1}{2}AD$. Estamos mais acostumados a provar igualdade de segmentos. Será que conseguimos transformar nosso problema em: "prove essa igualdade de segmentos"? Sim: considere $T$ o ponto médio de $AD$. Como $AT=\frac{AD}{2}$, basta mostrarmos que $AT=AC(*)$ para resolvermos o problema.

Agora, precisamos usar todos os fatos da figura. Como podemos usar que $M$ é o ponto médio de $BC$? Quais propriedades do ponto médios nós conhecemos? Uma delas é que as diagonais de um quadrilátero se encontram nos seus pontos médios se, e somente se, ele é um paralelogramo. O problema é que não temos um paralegramo ai cujas diagonais se encontrem em $M$. Isso não é problema: prolongue $AD$ por $D$ até o ponto $P$ de forma que $AM=MP$. Com isso, o quadrilátero $ABPC$ é um paralelogramo, pois suas diagonais $AP$ e $BC$ se encontram nos seus pontos médios (que no caso é $M$).

Essas novas construção nos dão informações importantes? Sim: observe em primeiro lugar que $T$ é ponto médio da hipotenusa do triângulo $ABD$. Assim $AT=BT=DT$. E isso é muito legal, afinal $AT$ está entre uma das medidas que queremos provar no final. E ela reaparece novamente em $BT$ e $DT$, ou seja, existe mais chance de termos alguma ideia que a envolva.

Além disso, outra medida que queremos mexer (no caso $AC$) é igual a $BP$ (olha aí uma das vantagens do paralelogramo: "transferimos medida"). Ou seja, basta mostrarmos que este último valor é igual a $AT$, $BT$ ou $CT$. De certa forma, existem várias maneiras de provarmos que $(*)$ é verdadeira. No caso, iremos mostrar que $BP=BT$. Como podemos fazer isto? Uma boa maneira é utilizarmos ângulos: se mostrarmos que $\angle BTP=\angle BPT$, então isto estará provado.

Vamos mexer com os ângulos da figura então. Existe alguma informação do enunciado que ainda não usamos? Sim: $\angle MAC = 2\angle BAM$. Considere $x=\angle BAM$. Então $\angle MAC=2x$. O interessante é se conseguirmos calcular $\angle BTP$ e $\angle BPT$ em função de $x$.

Como $ABPC$ é um paralelogramo, então $\angle BPT=\angle PAC = 2x$. Além disso, como $AT=BT$, segue que $\angle ABT = x$. Se aplicarmos o Teorema do Ângulo Externo no triângulo $ABT$, segue que $\angle BPT=2x$. Desta forma $BP=BT$, de onde segue que $(*)$ é verdadeira.

Exemplo (Cone Sul 1991)

Sejam $A$, $B$ e $C$ três pontos não colineares e $E$ ($\neq B$) um ponto arbitrário não pertencente a reta $AC$. Construa os paralelogramos $ABCD$ e $AECF$. Prove que $BE \parallel DF$.

Solução: Um bom desenho pode te ajudar a conjecturar algo: parece, pela figura, que $BF$ e $DE$ são paralelos. Desta forma, se provarmos que $BEDF$ é um paralelogramo, resolveremos o problema. Mas mexer com paralelismo parece um pouco chato. Só que, se provarmos que $BE=DF$ e $BF=DE$, então $BEDF$ será um paralelogramo.

Como podemos mostrar que $BE=DF$? Uma boa maneira é procurarmos alguma congruência na figura. Observe que $AD=CB$ e $AF=CE$. Parece que os triângulos $ADF$ e $CBE$ são congruentes. Se provarmos isto, a igualdade $BE=DF$ é mostrada. Para terminarmos de mostrar esta congruência, é suficiente provarmos que $\angle DAF= \angle BCE$.

Observe que

$\angle DAF= \angle FAC+ \angle CAD$

$\angle BCE = \angle BCA + \angle ACE$

Porém, $\angle FAC = \angle ACE$ e $\angle CAD = \angle BCA$ (pois eles são alternos internos). Desta forma, $\angle DAF= \angle BCE$, de onde segue que $ADF$ e $CBE$ são congruentes pelo caso $LAL$.

E para provarmos que $BE=DF$? Encontraremos outra congruência. Observe que $AF=CE$ e $AB=CD$. Logo, basta provarmos que $ABF$ e $CDE$ são congruentes. Para isto, é suficiente mostrarmos que $\angle BAF = \angle DCE$. Repare que

$\angle BAF= \angle FAC - \angle BAC$

$\angle DCE= \angle ACE - \angle ACD.$

Além disso, $\angle FAC = \angle ACE$ e $\angle BAC=\angle ACD$ (pois eles são alternos internos). Deste modo, $\angle BAF = \angle DCE$, de onde segue que os triângulos $ABF$ e $CDE$ são congruentes e assim $BE=DF$.

Portanto, $BEDF$ é um paralelogramo e $BE$ é paralelo a $DF$.

Lugares Para Estudar

• Quadriláteros Notáveis (POTI - Nível 2)
• Problemas Resolvidos: Quadriláteros Notáveis (POTI - Nível 2)

Vídeos

• Quadriláteros Notáveis (POTI - Nível 2)
• Caracterizações do Paralelogramo (POTI 2017)
• Quadriláteros Notáveis: Exercícios I (POTI 2017)
• Quadriláteros Notáveis: Exercícios II (POTI 2017)

Bibliografia

• BARBOSA, João Lucas Marques. Geometria Euclidiana Plana. 11ª. ed. [S.l.]: SBM, 2012. 257 p.
• A.S. Posamentier, C.T. Salkind : Challenging Problems in Geometry, Dover Publications, 1996.